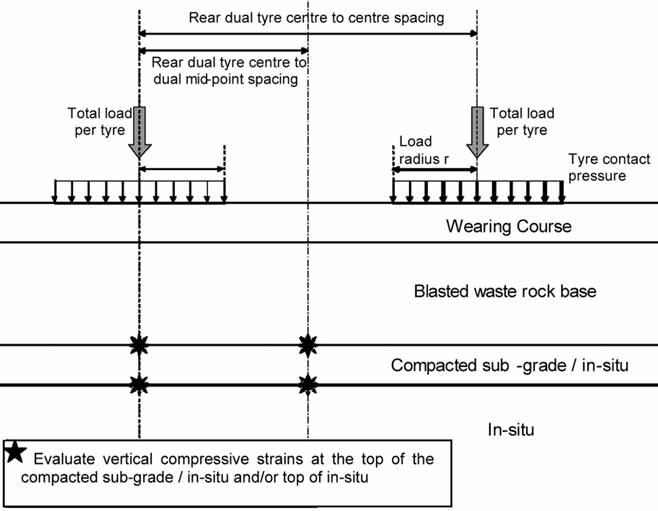
Figure 1—Multi-layer model for mechanistic structural design evaluation (in this case using a 4-layer model)
Building Better Haul Roads
Higher payloads and autonomous operations need roads designed for structural strength
By Dr. Roger J. Thompson

In truck-based hauling systems, the mine haul road network is a critical and vital component of the production process. As such, under-performance of a haul road will impact immediately on mine productivity and costs. Operations safety, productivity and equipment longevity are all dependent on well-designed, constructed and maintained haul roads.
Economies of scale and the increase in haul truck payload has so far seen the ultra-class truck population rise significantly. With this increasing size, haul road performance can be compromised, resulting in excessive total road-user costs; often seen directly as an increase in cost per ton hauled, but also indirectly as reduced production rates and vehicle and component service life.
As the concept of autonomous trucking moves from prototypes to production-ready applications, the operating performance of the haul road will become mission critical to the overall success of autonomy in mining. Rapid deterioration of road performance will require costly remediation, human intervention and significant, albeit temporary, changes to operating procedures, to accommodate these types of events. With autonomous trucking, vehicle path wander is minimal and the road will be subject to high channelized wheel loads over a very limited area, without the wheelpath variations often encountered with conventional trucking.
Many concepts from highway engineering can be adapted to the design, construction and management of mine roads. However, significant differences in applied loads, traffic volumes, construction material quality and availability, together with design life and road-user cost considerations, indicate a custom-made design solution is required.
The operating performance of a mine road can be subdivided into four distinct design components and when designing and constructing a haul road for optimal performance, these design components are best addressed using an integrated approach. If one design component is deficient, the other components may not work to their maximum potential and road performance is often compromised. The cure, however, is not necessarily just 'more frequent maintenance;' no amount of maintenance will fix a poorly designed road.
Haul road design should follow an integrated approach, based on the geometric, structural (layerworks), functional (wearing course) and maintenance management components. Once the geometric design is finalized, and the in-situ or sub-grade along the proposed alignment of the road determined, the structural design can begin. The structural design provides haul road strength to carry the imposed wheel loads over the design life of the road without the need for excessive maintenance, often caused by deformation of one or more layers in the road—most often soft, weak or wet in-situ or sub-grade materials below the road surface.
CBR Cover-curve Design
The California Bearing Ratio (CBR) covercurve design method, developed in 1942
and adapted by the U.S. Bureau of Mines
(USBM) haul road design guidelines developed in 1977, has been widely applied to
the design of mine haul roads in which
untreated materials are used and is based
on the CBR penetration test.
The CBR of a material is expressed as a percentage of the penetration resistance of that material compared to that of a standard value for crushed stone. The value is normally derived from laboratory tests, although field impact and penetration testing also delivers indirect CBR values. In all but arid and semi-arid environments, the CBR value adopted in the design should be based on a soaked CBR test. In this empirical design procedure, pavement cover thickness above a material with a particular CBR was determined as a function of applied wheel load and the CBR of the material. The same technique can be used for successive layers—the only requirement being that successive layers must be of higher CBR than the preceding layer and the change in CBR not too abrupt, since the preceding layer acts as a compaction anvil for the subsequent layer.
Equation 1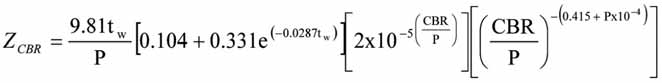
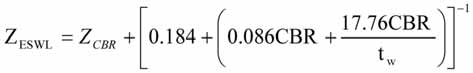
Equation 2
Although the CBR cover-curve approach has generally been superseded by a mechanistic approach, there are some design cases where it would still be appropriate. The USBM - CBR design criteria has been extended to accommodate wheel loads generated by typical ultra-class six- wheeled rear-dump trucks. The USBM work only extended to a 55-mt (300 mtGVM) truck size and does not incorporate the effects of tire pressure, which influence the bearing pressure and contact radius. The approximate CBR values of various in-site or sub-grade (unimproved) soil types are defined by the Unified Soil Classification (USCS), following Test Designation D-2487 of the American Society for Testing and Materials (ASTM) and the American Association of State Highway and Transportation Officials' (AASHTO) systems.
The equivalent single wheel load (ESWL) is the single wheel load having the same contact pressure, which produces the same value as the dual wheel loads at any depth in the layerworks. In the original USBM work, it was suggested that to accommodate the effects of dual rear wheel assemblies, single wheel loads should be increased by 20%. However, as will be seen later, when using the semi-rational ESWL approximation, a more realistic estimation can be made.
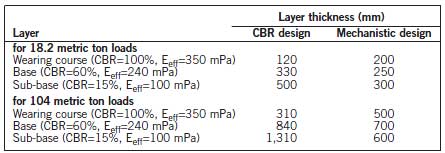
As an example, using USBM (1977) data for a 40,000 lb (18.2 mt) (single) wheel load, with a sub-grade (in-situ) CBR of 5%, at least 700-mm cover is required above this material. When a sub-base layer of CBR 15% material is placed above sub-grade, this layer should have 350-mm cover, in other words, the sub-base should be 350-mm (700-350) thick. Using a base layer CBR of 60% above this, the layer thickness will be 200 mm (350-150). A material of CBR of 100% would form the remaining 150 mm, to give total cover of 700 mm (350 + 200 + 150). When calculating the ESWL cover, a 20% increase in wheel load equates to approximately 790 mm of cover.
Alternatively Equation 1 can be used to estimate the thickness of cover (ZCBR (m)) required above a material of California Bearing Ratio (CBR %).
In Equation 1; tw is the truck wheel load (mt), P is tire pressure (kPa) and CBR is the California Bearing Ratio of the material (%). To replicate the tandem rear axle, the ESWL (ZESWL (m)) cover can be estimated using Equation 2.
The above equations have been developed for truck wheel loads in the range of 15 to 105 mt (equivalent to a GVM of 90 to 630 mt) and a tire pressure ranging from 700 to 900 kPa. Applying the above equations to the previous example yields an ESWL cover of 950 mm and a sub-base thickness of 500 mm. The base layer could then be placed at 330 mm thickness, followed by the wearing course at 120 mm thickness. Using the semi-rational ESWL approximation therefore yields a slightly more conservative estimate of layer thickness requirements.
Mechanistic Design Methodology

The applied load is calculated according to the mass of the vehicle and the rear dual wheel axle load distributions, from which the single wheel load is found. The load application is determined from dual wheel geometry and together with tire pressure, the contact stress is calculated. Figure 1 summarizes the layered elastic model and data requirements.
The strains induced in a road are a function of the effective elastic (resilient) modulus (Eeff) values assigned to each layer in the structure. Other correlations are published by Thompson and Visser and AUSTROADS from where Equation 3 is taken, which, when used in conjunction with layer CBR values, determines the modulus values (Eeff, MPa).
In each case however, care should be taken to ensure that the general correlations presented here are consistent with soil properties not directly assessed in the derivation of the equation. In several instances, the Eeff values actually measured in mine haul roads have been found to be well in excess of those predicted by Equation 3, especially on laden carriageways where traffic-induced compaction has occurred following construction.
Mechanistic Design Criteria
Highway vertical compressive strains are
limited through design to about 1,000 to
1,500 microstrain, but for mine haul roads,
higher limits can be applied since:
• Load repetitions are much lower
(albeit at higher wheel loads) than for
highways;
• Design life may be much shorter; and
• Blading can be easily undertaken; and
combined with occasional re-sheeting,
can be used to correct permanent
deformations in all but the most
inadequately designed roads.
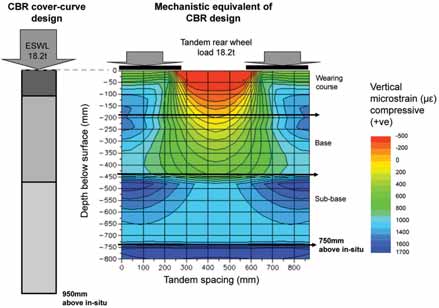
Comparative Analysis: CBR Cover-Curve vs. Mechanistic Design
To compare the two design methodologies, a range of layerworks materials and
wheel loads are required. Initially, the
previous example is adopted (18.2 metric ton wheel load) with similar in-situ
and layer strengths. Tandem wheel geometry for a CAT 773F (16.4-mt wheel load
similar to the required 18.2 mt) is used
and an 800-kPa tire pressure is applied.
Using the MePADS software to solve the 4-layer model with the depth to base of sub-grade set at 5-m below the surface of the road gives the comparative results shown in Figure 3. For the layer thicknesses determined from the CBR cover-curve design methodology, the highest strain value was 2,160 microstrain at the top of the subbase, while the sub-grade strain was limited to 1,400 microstrain. By redefining layer thicknesses to meet the 2,000 microstrain limit, a new mechanistic structural design was determined (See Table 1 and Figure 3). A 200-mm reduction in layer thickness was achieved, which, when combined with a haul road construction width of 27 m, would achieve a savings in material placement and compaction of approximately 5,400 m3/km or 21%.
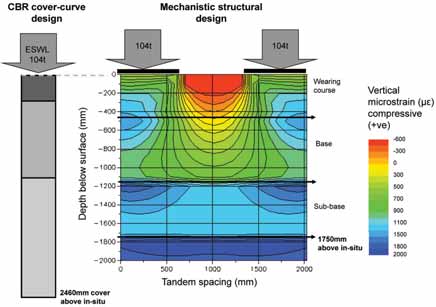
Using the MePADS software to solve the 4-layer model, with depth to base of sub-grade set at 5-m below the surface of the road, a tandem wheel geometry for a CAT 797B (104 mt wheel load) is used and an 800 kPa tire pressure are applied. The CBR cover-curve design results in strains in excess of the 2,000 microstrain limit being developed in the base and sub-base, which will compromise road serviceability and performance. The mechanistically-derived equivalent design reduces base and sub-base thickness by 850 mm, and increases wearing course thickness by 190 mm. The overall savings in material volumetric and compaction requirements is 660 mm. When combined with a haul road construction width of 34 m, this would achieve a savings in material placement and compaction of approximately 22,440 m3/km or 27% and also provides a better response to the applied wheel loads.
For the larger wheel loads in this example, the CBR cover-curve ESWL-based approach leads to significant under-design of Category I and II roads compared to the mechanistically-derived equivalent structure. While the method could be appropriate for Category III roads, the excessive material volumetric and compaction requirements indicate the method is also inappropriate under these circumstances too.
In the foregoing analysis, it is also important to recognize the role of layer compaction in the development of the design and if different layer material resilient moduli are used, the comparative design results will also vary. Additionally, the mechanistic design approach is also sensitive to the assumed depth to base of sub-grade material. In this analysis, the depth was limited to 5 m. Critically, should this depth reduce (and the thickness of the sub-grade layer reduces), the stresses and strains induced in this layer by the applied wheel load will increase, requiring a change to the layerworks design.
Conclusions
The structural design specification of a
mine haul road is a critical component in
the overall road design process. Poor
design often leads to premature failure of
the road, safety is often compromised
and productivity and equipment service-life will certainly decrease. With the
advent of autonomous trucks, any structural design deficiency would be exacerbated and its impact on operations more
problematic to address.
Two approaches are available to the design engineer; the CBR cover-curve methodology, derived and updated from the seminal USBM work in 1977 and more recently, a mechanistic design methodology utilizing a multi-layered elastic model to represent the response of the haul road layerworks to an applied load.
When comparing the two design techniques, it is seen that for smaller truck wheel loads, the CBR cover-curve ESWL-based design yields a slightly underdesigned result compared to the mechanistic design. Therefore, the CBR cover-curve design method could be used to design Category III roads, albeit at the expense of a potential 21% saving in layerworks volumetric and compaction requirements that a mechanistic design would deliver.
When much larger wheel loads are considered, in conjunction with the channelized traffic paths typical with autonomous trucks, the CBR cover-curve ESWL-based approach leads to significant under-design of Category I and II roads. While the method could be appropriate for Category III roads, the excessive material volumetric and compaction requirements indicate the method is inappropriate and a mechanistic approach is required under these circumstances.
Author Information
Thompson is Professor of Mining Engineering
for Curtin University at the Western
Australian School of Mines in Kalgoorlie,
Western Australia. He can be reached at:
r.thompson@curtin.edu.au. This article was
adapted from Thompson's presentation at the
Haulage & Loading 2011 conference, held
during May in Phoenix. The entire presentation, and others, can be accessed for a fee at
www.haulageandloading.com.